Valószínűségszámítás!

Első példa

Egy középiskolában két végzős osztály van. A osztályba 11 lány és 13 fiú, a 12. B osztályába 15 lány és 10 fiú tanuló jár. A 12. A osztály és a 12. B osztály is véletlenszerűen kijelöl egy-egy diákot arra, hogy a ballagási ünnepségen az osztályuk nevében elmondja a búcsúzó beszédet. Mekkora annak a valószínűsége, hogy mindkét tanuló lány? Egy újságíró interjút készít az érettségiről. Véletlenszerűen kiválaszt két végzős diákot. Mekkora a valószínűsége, hogy mindkét tanuló lány?

Megoldás;

Az A osztály létszáma 24 fő, a B osztályé pedig 25 fő. A beszéd megtartására összesen 24⋅25=600

 külön­böző módon választhatnak a két osztályból egy-egy diákot. Az A osztályból 11-féleképpen, a B-ből 15-féleképpen választhatnak lányt, vagyis a két lány választására 11⋅15=165  különböző lehetőségük van. 

 A valószínűség kiszámítása

   

A kérdezett valószínűség tehát 0,275

Az újságíró a 49 tanuló közül választ ki kettőt,  tehát az egyenlően valószínű lehetőségek száma: 

A két osztályban összesen 26 lány van, közülük bármelyik kettő egyenlő valószínűséggel választható, 

tehát a kedvező esetek száma 

a kérdezett valószínűség pedig 

Második példa

Feladat: 32 lapos kártyacsomagból kapunk 2 lapot.

Mi a valószínűsége annak, hogy a 2 lap közül:

az első király és a második ász

az egyik király, a másik ász

az első király

mindkettő király

nincs közte király

van közte király

legalább az egyik király

legfeljebb az egyik király

 

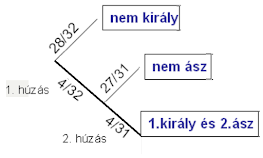
Megoldás: A kísérlet: 32 lapos kártyacsomagból kiveszünk 2 lapot (visszatevés nélkül) és megfigyeljük a lap figuráját. Ezért tisztázzuk, hogy a 32 lap között van 4 király + 4 ász + 24 se nem király, se nem ász. Megállapítjuk, hogy a 3 részhalmaz páronként egymást kizáró.

P(az első király és a második ász) =

= P(az első király) × P(a második ász, feltéve, hogy 1 királyt már húztunk) = 4/32 × 4/31

ui. az 1. lap kihúzásánál az összes lap közül választunk, és a kedvező lapok száma 4, de a 2. lap kihúzásánál már csak 31 lapból húzunk, és a kedvező lapok száma még mindig 4, mert nem ász volt az első.

Lássuk az ábrát: 

P (az egyik király és a másik ász) =

= P(az első király és a második ász vagy az első ász és a második király) =

= P(az első király) × P(a második ász feltéve, hogy 1 királyt már húztunk) +

+ P(az első ász) × P(a második király feltéve, hogy 1 ászt már húztunk)=

= 4/32 × 4/31 + 4/32 × 4/31 = 2. 4/32 × 4/31

Érdemes az urnamodellel számolni a későbbiekben is, amikor a sorrend tetszőleges:

P(1 király és 1 ász, amikor 32 lap közül 2-t kiveszünk) =

P(az első király) = P(az első király és a második tetszőleges) =

P(az első király) × P(a második bármi feltéve, hogy 1 királyt már húztunk) =

= 4/32 × 31/31 = 4/32

ui. az 1. lapnál az összes lap közül választunk, és a kedvező lapok száma 4, de a 2. lapnál már csak 31 lapból húzunk, és a kedvező lapok száma szintén 31, hiszen a 2. lap bármilyen lehet.

P(mindkét lap király) = P(az első király és a második király) =

= P(az első király) × P(a második király feltéve, hogy 1 királyt már húztunk) =

= 4/32 × 3/31

ui. az 1. lapnál az összes lap közül választunk, és a kedvező lapok száma 4, de a 2. lapnál már csak 31 lapból húzunk, és a kedvező lapok száma már csak 3, mert király volt az első is.

Az urnamodell szerint: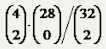 

P(nincs közte király) = P(az első nem király és a második sem király) =

= P(az első nem király) × P(a második nem király feltéve, hogy 1 nem királyt már húztunk) = 28/32 × 27/31

ui. az 1. lapnál az összes lap közül választunk, és a kedvező lapok száma 32-4, de a 2. lapnál már csak 31 lapból húzunk, és a kedvező lapok száma már 1-el kevesebb, mint az 1. húzásnál.

Az urnamodell szerint; 

P(van közte király) = P(1 vagy 2 király van közte) = 1 - P(nincs közte király)

Az ellentett esemény segítségével gyorsabban felírható, mert azt már kiszámoltuk.

Tehát: 1 - 28/32 × 27/31

Az urnamodell szerint: 

P(legalább az egyik király) = P(van közte király)

Jelentése: pontosan 1 vagy pontosan 2 király van a 2 lap között.

Tehát megegyezik az előző eredménnyel.

P(legfeljebb az egyik király) =

= P(0 vagy 1 király van közte) = 1 - P(mindkét lap király)

Urnamodell!